Угол между ребром и плоскостью является важным понятием в геометрии. Он определяется как угол между направляющим вектором ребра и нормальным вектором плоскости. В этой статье мы рассмотрим методы для нахождения угла между ребром и плоскостью на основе указанных векторов. Подробнее про то как найти угол между ребром и плоскостью Вы можете почитать на сайте: https://znaniyaotvet.ru
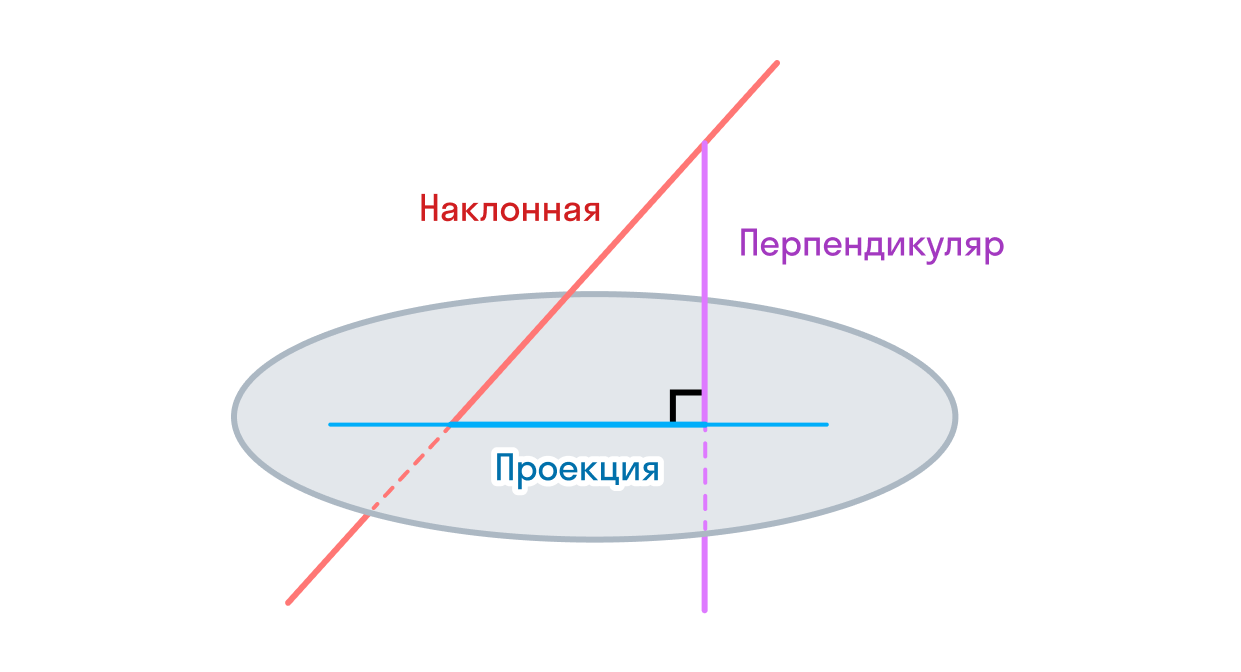
1. Определение направляющего вектора ребра
Направляющий вектор ребра может быть найден с помощью вычитания координат второй конечной точки ребра из координат первой конечной точки.
Пусть ребро A имеет начальную точку A1(x1, y1, z1) и конечную точку A2(x2, y2, z2). Направляющий вектор ребра A будет определен как:
A = (x2 — x1, y2 — y1, z2 — z1)
2. Определение нормального вектора плоскости
Нормальный вектор плоскости определяется с помощью уравнения плоскости. Пусть плоскость задана уравнением Ax + By + Cz + D = 0, где A, B, C и D — коэффициенты уравнения плоскости. Тогда нормальный вектор плоскости будет равен (A, B, C).
3. Нахождение угла между векторами
После нахождения направляющего вектора ребра и нормального вектора плоскости можно найти угол между ними с использованием следующей формулы:
cos θ = (A · B) / (|A| · |B|)
где θ — искомый угол, A — направляющий вектор ребра, B — нормальный вектор плоскости, A · B — скалярное произведение векторов, |A| и |B| — длины векторов.
4. Расчет угла
Для расчета значения угла можно использовать арккосинус функцию. Результат будет представлен в радианах. В случае необходимости его можно преобразовать в градусы.
5. Пример
Давайте рассмотрим пример нахождения угла между ребром и плоскостью. Пусть ребро A определено начальной точкой A1(1, 2, 3) и конечной точкой A2(4, 5, 6). Плоскость B задана уравнением 2x + 3y + 4z + 5 = 0.
Сначала найдем направляющий вектор ребра A:
A = (4 — 1, 5 — 2, 6 — 3) = (3, 3, 3)
Далее найдем нормальный вектор плоскости B:
B = (2, 3, 4)
Затем найдем скалярное произведение векторов A и B:
A · B = (3 · 2) + (3 · 3) + (3 · 4) = 6 + 9 + 12 = 27
Теперь найдем длины векторов A и B:
|A| = sqrt((3)^2 + (3)^2 + (3)^2) = sqrt(9 + 9 + 9) = sqrt(27)
|B| = sqrt((2)^2 + (3)^2 + (4)^2) = sqrt(4 + 9 + 16) = sqrt(29)
Наконец, найдем значение угла:
cos θ = (27) / (sqrt(27) · sqrt(29)) ≈ 0.9009
θ ≈ acos(0.9009) ≈ 0.4488 радиан ≈ 25.72 градуса
Заключение
Найдение угла между ребром и плоскостью является важной задачей в геометрии. Оно может применяться в различных областях, включая компьютерную графику, архитектуру и инженерию. В данной статье мы описали методы для нахождения этого угла на основе направляющего вектора ребра и нормального вектора плоскости.